Divisione di un poligono regolare

[Maurizio59]

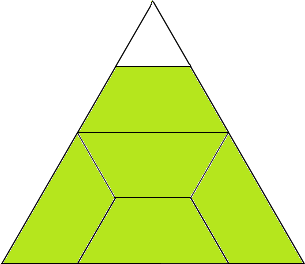
Un poligono regolare di area 1 è diviso in parti uguali di area massima.
Consideriamo i seguenti casi:
1) Triangolo equilatero in cinque parti.
2) Esagono regolare in sette parti.

[Gianfranco]

Mi sembra che del triangolo equilatero in 5 parti triangolari uguali ne abbiamo già discusso qui: viewtopic.php?f=1&t=8547
Potrebbe essere un punto di partenza.
Le "parti uguali" di cui si parla in questo post però non sono necessariamente triangoli.

[Quelo]

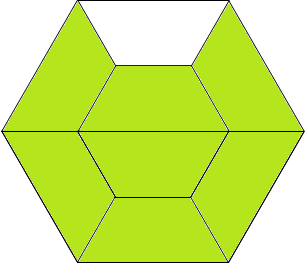
La prima cosa a cui ho pensato è stata "Figure esagonali composte da esagoni regolari"
In questo caso l'area è 1/9

Un'altra possibilità è questa, qui l'area è 0,11533

Esagonoin7.png (55.85 KiB) Visto 104065 volte

[Maurizio59]

Per il triangolo possiamo partire da questa divisione con area uguale a 3/16 = 0.1875.



Visto che un esagono regolare può essere diviso in otto parti uguali come in figura



si può partire da un valore dell'area di 1/8 = 0.125.

[Gianfranco]

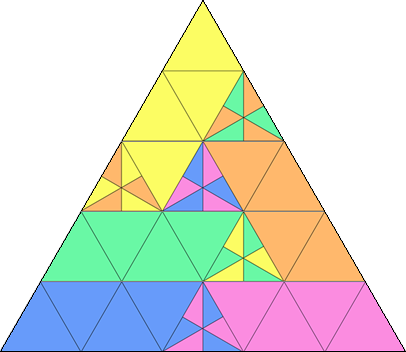
Complimenti a Quelo e Maurizio59, belle soluzioni!
A quanto pare, la soluzione di Maurizio sul triangolo migliora quella data da Quelo in un post precedente.
A questo punto, con poca fatica, adatto la soluzione di Quelo all'esagono:

esa7parti.png (132.34 KiB) Visto 103464 volte

In questo caso sono 42 triangoli raggruppati a gruppi di 6.
Il numero di triangoli si può aumentare, basta che sia multiplo di 7.
Al limite, la copertura è uguale a quella del cerchi inscritto:
Se non sbaglio, l'area di ciascuna parte è 0,129558...

[franco]

...
Al limite, la copertura è uguale a quella del cerchi inscritto:
Se non sbaglio, l'area di ciascuna parte è 0,129558...

Il problema chiede che l'esagono sia diviso in "parti uguali", non necessariamente parti poligonali.
Quindi il cerchio diviso i 7 settori credo vada benissimo senza bisogno di limiti
Forse, nel cerchio si possono anche fare 7 gobbette equidistanti ed aumentare ancora un filino l'area dei settori.

[Maurizio59]

...
Il problema chiede che l'esagono sia diviso in "parti uguali", non necessariamente parti poligonali.
Quindi il cerchio diviso in 7 settori credo vada benissimo senza bisogno di limiti
Forse, nel cerchio si possono anche fare 7 gobbette equidistanti ed aumentare ancora un filino l'area dei settori.

Il cerchio inscritto nell'esagono diviso in 7 settori circolari uguali va benissimo.
In questo caso l'area vale $\frac{\pi}{14\sqrt3}=0.129557...$

Non sono ammesse però parti "disconnesse".
In questo caso il triangolo può essere completamente diviso in 5 parti uguali come in figura

[Gianfranco]

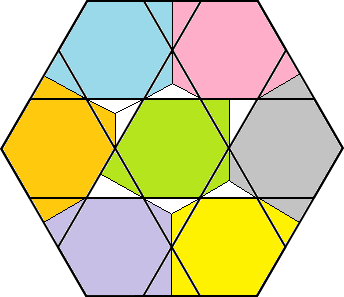
Bella la soluzione del matematico russo Mikhail Patrakeev.
Alcuni pezzi sono disconnessi ma ce ne sono altri connessi in parte.
Mi chiedo se si può inventare una dissezione in cui ciascuna parte sia connessa almeno per punti singoli.
A questo proposito c'è una soluzione geometrico-artistica dell'artista-matematico ucraino Pavel Guzenko che mostra come dividere un triangolo equilatero in 15 parti congruenti connesse(?) E 15 è un multiplo di 5.

guzenko.png (76.29 KiB) Visto 102862 volte

Sarebbe bello unire le idee di un matematico russo e un artista ucraino per trovare una bella soluzione a questo problema.
Io credo che i popoli vogliano la pace. Sono i governanti a mandare le persone a fare la guerra. Scusate per la digressione.

[Gianfranco]

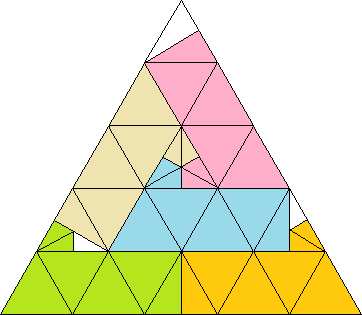
Ho separato le 5 parti della soluzione di Mikhail Patrakeev.
Quattro di esse sono congruenti per traslazione e rotazione.
Una, quella rosa, è congruente alle altre ma richiede anche un ribaltamento, cioè la terza dimensione.
E' ammesso questo?
Che ne pensate?

tri5sim.png (61.53 KiB) Visto 102838 volte

[Maurizio59]

Suggerimento.

La prima cosa a cui ho pensato è stata "Figure esagonali composte da esagoni regolari"
In questo caso l'area è 1/9
...

Buona intuizione.
Essa si può migliorare (vedi figura) portando l'area a 7/54 = 0.1296...

Con alcuni accorgimenti l'area diventa 11/81 = 0.1358...

Ma essa può ancora essere migliorata...

[Quelo]

Potrebbe essere così?

hexagon-in-7-parts-3.png (23.33 KiB) Visto 100843 volte

$\displaystyle A=\frac{5}{36}=0,13\overline{8}$

[Gianfranco]

Quelo e Maurizio: risultati meravigliosi!

[Maurizio59]

Potrebbe essere così?
...

Sì, è così.
Ora resta solo il triangolo.

[Gianfranco]

Per esempio, col triangolo?

Tridiv5.png (19.03 KiB) Visto 99567 volte

A=41/216 = 0,1898...

[Maurizio59]

Per esempio, col triangolo?
...

Bella soluzione, Gianfranco.
Ecco una soluzione simile alla tua.

L'area è 29/150 = $0.19\overline{3}$

Ma, cambiando approccio, si può fare ancora meglio.