Caro franco, quando due ragionamenti probabilistici portano a due risultati diversi o uno dei due è sbagliato o sono sbagliati entrambi; vi è tuttavia una terza possibilità: i ragionamenti si riferiscono a problemi diversi!
Inutile dire che io trovo un risultato diverso dal tuo quindi, per spazzare dal campo la terza possibilità, provvedo ad illustrare il problema che ho affrontato io.
Un mazzo di carte è formato da quattro semi di dieci carte ciascuno. Potrebbero anche essere un numero diverso di semi con un numero diverso di carte per ciascun seme ma restiamo nel caso particolare.
Quando "mescoliamo" il mazzo produciamo (o vorremmo produrre) una permutazione casuale delle quaranta carte. Questa permutazione può anche essere considerata una parola di quaranta lettere prese da un alfabeto di quattro lettere (o anche un numero di quaranta cifre in base $5$): queste permutazioni sono
$\frac{\text permutazioni di 40 carte} {\left({\text permutazioni di 10 carte}\right)^{\script 4}} \/=\/ \frac {40!} { 10! 10! 10! 10!} \/=\/ 4705360871073570227520 \/\approx\/ 5 \/\times\/ 10^{\script 21}$
un numero finito, grande ma non grandissimo.
Gli oggetti distinti che cerchiamo di enumerare sono dunque le possibili successioni di carte; nessuna informazione in nostro possesso consente di distinguere a priori queste permutazioni quindi è naturale assegnare a ciascuna di esse la stessa probabilità in base al principio di indifferenza: ecco i nostri casi possibili (equiprobabili).
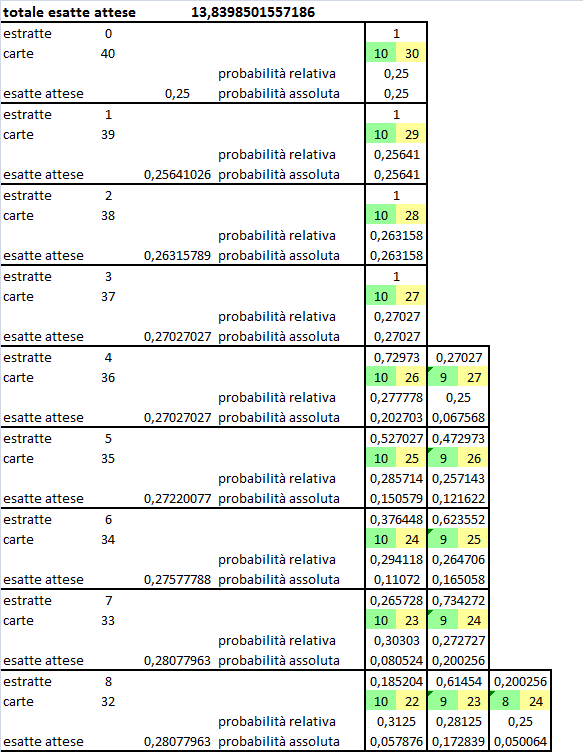
Quando scopriamo la prima carta apprendiamo soltanto che la permutazione attuale appartiene al sottoinsieme di quelle che cominciano con una carta di quel seme perché nessuna informazione in nostro possesso lega il seme della prima carta a quello della carta successìva (eccezion fatta per la numerosità delle carte di quel seme). Ecco quindi che, a questo punto, ci ritroviamo con una parola di trentanove lettere di cui non sappiamo ancora nulla eccetto la composizione $\left\{9,10,10,10\right\}$.
Questo è il mio scenario: se siamo d'accordo su di esso allora i nostri ragionamenti devono raggiungere lo stesso risultato anche se sono diversi.
Supponiamo ora di avere scoperto quattro carte: qual è la probabilità che siano presenti tutti e quattro i semi?
Vi sono ovviamente $10$ modi di scegliere una carta di ciascun seme ma quanti sono i modi di scegliere $4$ carte dal mazzo? Sono
${40 \choose 4}\/=\/91390$
e, dato che tutte queste permutazioni sono equiprobabili la probabilità cercata non può essere che
$p\left(1111\/|\/4\/I\right)\/=\/\frac{{10 \choose 1}{10 \choose 1}{10 \choose 1}{10 \choose 1}}{{40 \choose 4}}\/=\/\frac{10000}{91390}\/=\/\frac{1000}{9139}$
Nel simbolo della probabilità $1111$ sta per "è presente una carta per ciascun seme" e la condizione $4$ dopo la barra verticale significa "dopo che sono state scoperte quattro carte".
Ovviamente, la probabilità che almeno due carte siano dello stesso seme è
$p\left(\overline{1111}\/|\/4\/I\right)\/=\/1\/-\/p\left(1111\/|\/4\/I\right)\/=\/\frac{8139}{9139}$
e la probabilità di indovinare il seme della quinta carta è
$p\left(S\/|\/\overline{1111}\/4\/I\right) \/\times\/ p\left(\overline{1111}\/|\/4\/I\right) \/+\/ p\left(S\/|\/1111\/4\/I\right) \/\times\/ p\left(1111\/|\/4\/I\right) \/=\/ \frac{10}{36} \/\times\/ \frac{8139}{9139} \/+\/ \frac{9}{36}\/ \times\/ \frac{1000}{9139} \/=\/ \frac{15065}{54834} \/=\/ 0,2747\ldots$
e non $10/37 \/=\/ 0,2702\ldots$ come sostieni tu.
Supponiamo ora che siano state scoperte $k_1{\script }$ carte del primo seme, $k_2{\script }$ del secondo, $k_3{\script }$ del terzo e $k_4{\script }$ del quarto, per un totale di $k$ carte: per quanto visto sopra la probabilità sarà
$p\left(k_{\script 1} k_{\script 2} k_{\script 3} k_{\script 4} \/|\/ k\/I\right) \/=\/ \frac {{10 \choose k_{\script 1}} {10 \choose k_{\script 2}} {10 \choose k_{\script 3}} {10 \choose k_{\script 4}}} {{40 \choose k}}$
Riordinando i fattoriali dei coefficienti binomiali possiamo vedere la cosa in una luce un po' diversa
$p\left(k_{\script 1} k_{\script 2} k_{\script 3} k_{\script 4} \/|\/ k\/I\right) \/=\/ \frac {\frac {k!} {k_{\script 1}! k_{\script 2}! k_{\script 3}! k_{\script 4}!} \quad \frac {\left(40-k\right)!} {\left(10-k_{\script 1}\right)! \left(10-k_{\script 2}\right)! \left(10-k_{\script 3}\right)! \left(10-k_{\script 4}\right)!} } {\frac {40!} { 10! 10! 10! 10!} }$
In cui i multinomiali sono
$\frac {k!} {k_{\script 1}!k_{\script 2}!k_{\script 3}!k_{\script 4}!} \/=\/ \frac {{\text permutazioni di }k \quad{\text carte}} {\prod_{\script i} {\text permutazioni di }k_{\script i} \quad{\text carte}}$
$\frac {\left(40-k\right)!} {\left(10-k_{\script 1}\right)!\left(10-k_{\script 2}\right)!\left(10-k_{\script 3}\right)!\left(10-k_{\script 4}\right)!} \/=\/ \frac {{\text permutazioni di }40-k \quad {\text carte}} {\prod_{\script i} {\text permutazioni di }10-k_{\script i} \quad{\text carte}}$
e, come sopra
$\frac {40!} { 10! 10! 10! 10!} \/=\/ \frac{\text permutazioni di 40 carte} {\left({\text permutazioni di 10 carte}\right)^{\script 4}}$
Così abbiamo esplicitato che i casi possibili sono proprio le nostre permutazioni.
Ma se noi siamo in grado di assegnare la probabilità di una qualsiasi combinazione di carte scoperte allora non ci resta che assegnare la probabilità di indovinare il seme data quella combinazione di carte:
$p\left(S \/|\/ k_{\script 1} k_{\script 2} k_{\script 3} k_{\script 4} \/ k\/I\right) \/=\/ \frac {\max\left(10 - \left\{ k_{\script 1}, k_{\script 2}, k_{\script 3}, k_{\script 4}\right\}\right)} {40 - k}$
e calcolare il valore atteso per il numero di volte in cui il seme viene indovinato
$\sum\/_{\script \left\{ k_{\script 1}, k_{\script 2}, k_{\script 3}, k_{\script 4}\right\} \neq \left\{ 10,10,10,10 \right\}}{ p\left(S \/|\/ k_{\script 1} k_{\script 2} k_{\script 3} k_{\script 4} \/ k\/I\right) \/\times\/ p\left(k_{\script 1} k_{\script 2} k_{\script 3} k_{\script 4} \/|\/ k\/I\right) }$
La sommatoria è estesa a tutte le quadruple di $k_{\script i$ inclusa $\left \{0, 0, 0, 0\right\}$ ed esclusa ovviamente $\left \{10, 10, 10, 10\right\}$.
Non sarà elegante come una forma chiusa ma può essere calcolato a mano per piccoli numeri e con un personal computer per numeri non troppo grandi: nel nostro caso
$\frac {334360818419} {22797966620} \/=\/ 14,66625\ldots$
Certo, questo valore non concorda con quello trovato con una simulazione da quell'utente di Matematicamente. Ma, come dire, quando una previsione basata sulla logica e una simulazione non concordano può ben darsi che sia sbagliata la simulazione: fare buone simulazioni non è per nulla facile e inoltre bisognerebbe avere almeno dei riscontri con casi più semplici in cui sia possibile calcolare il risultato in modo indipendente.
Comunque, non sapendo come fosse stata fatta detta simulazione me ne sono fatta una mia utilizzando R (un software statistico open source disponibile gratuitamente in rete).
Ecco il codice oppotunamente commentato (i commenti precedono ciò a cui si riferiscono)
# ---------------------------------------------------------------------------- #
# - numero di ripetizioni nella simulazione: 1000000 - #
# ---------------------------------------------------------------------------- #
numRip <- 1e6
# ---------------------------------------------------------------------------- #
# - vettore con il numero di carte indovinato in ciascun giro - #
# ---------------------------------------------------------------------------- #
tt <- numeric(0)
# ---------------------------------------------------------------------------- #
# - ciclo principale della simulazione - #
# ---------------------------------------------------------------------------- #
while (length(tt) < numRip) {
# ---------------------------------------------------------------------------- #
# - vettore che contiene gli esiti del ciclo del mazzo: - #
# - t
== 1 se il seme della carta i-esima è stato indovinato - #
# - t == 0 in caso contrario - #
# ---------------------------------------------------------------------------- #
t <- numeric(40)
# ---------------------------------------------------------------------------- #
# - permutazione casuale di 40 elementi [sample(40)] riportata alle decine - #
# - [%/% 10]: - 1 perché [%/% 10] dà 0 da 0 a 9, dà 1 da 10 a 19 ecc.; + 1 - #
# - perché voglio i semi da 1 a 4 e non da 0 a 3. - #
# - [%/%] è la divisione intera - #
# ---------------------------------------------------------------------------- #
m <- 1 + (sample(40) - 1)%/%10
# ---------------------------------------------------------------------------- #
# - numero di carte iniziale di ciascun seme: c(10,10,10,10) - #
# ---------------------------------------------------------------------------- #
k <- rep(10, 4)
# ---------------------------------------------------------------------------- #
# - contatore della carta girata - #
# ---------------------------------------------------------------------------- #
i <- 0
# ---------------------------------------------------------------------------- #
# - ciclo di scorrimento del mazzo - #
# ---------------------------------------------------------------------------- #
while (i < 40) {
# ---------------------------------------------------------------------------- #
# - incremento il contatore (cioè giro una carta) - #
# ---------------------------------------------------------------------------- #
i <- i + 1
# ---------------------------------------------------------------------------- #
# - il seme della carta i-esima è indovinato quando è uguale al primo dei - #
# - semi con un numero di carte non inferiore a quello degli altri. - #
# - which (condizione) produce un vettore che contiene gli indici corri- - #
# - spondenti a valori del vettore target che soddisfano la condizione: - #
# - se, per esempio, k == c(10,10,10,10), which(k == max(k)) produce - #
# - c(1,2,3,4); se k == c(6,3,6,1), otteniamo c(1,3); se k == c(1,2,3,4) - #
# - ottengo c(4): mettendo [1] prendo il primo elemento del vettore - #
# ---------------------------------------------------------------------------- #
t <- m == which(k == max(k))[1]
# ---------------------------------------------------------------------------- #
# - diminuisco di 1 il numero di carte del seme di m - #
# ---------------------------------------------------------------------------- #
k[m] <- k[m] - 1
} # fine ciclo piccolo
# ---------------------------------------------------------------------------- #
# - aggiungo il numero di carte indovinate in questo giro al vettore - #
# ---------------------------------------------------------------------------- #
tt <- c(tt, sum(t))
} # fine ciclo grande
# ---------------------------------------------------------------------------- #
# - stampo l'expectation - #
# ---------------------------------------------------------------------------- #
print(paste(mean(tt), " +/- ", sd(tt), " (N = ",numRip,")", sep=""))
# ---------------------------------------------------------------------------- #
# - istogramma degli esiti - #
# ---------------------------------------------------------------------------- #
hist(tt, breaks=(1:40), prob=TRUE, main="distribuzione degli esiti",
xlab="numero di carte indovinate", ylab="frazione")
Il risultato della simulazione è: $14,67 \/\pm\/ 2,15 \/ \left(N \/=\/ 1000000\right)$ con la seguente distribuzione
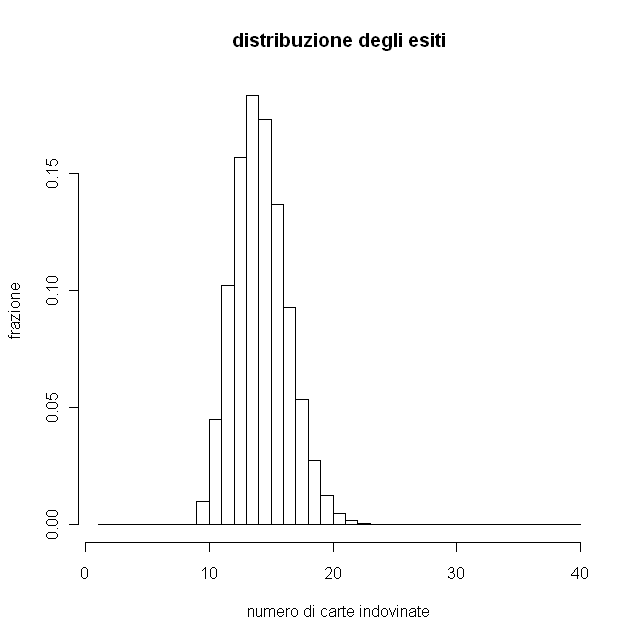
Forse $10^{\script 6}$ ripetizioni potranno sembrare esagerate ma occorre ricordare che i casi possibili sono $\approx\/ 5 \/\times\/ 10^{\script 21}$.
Sono quindi abbastanza confidente nel mio risultato.
A proposito, il metodo è del tutto generale: il mazzo sia composto di $s$ semi ciascuno con $n_{\script i}$ carte per un totale di $n$; ne peschiamo $k_{\script i}$ di ciascun seme per un totale di $k$ con una probabilità pari a
$p\left(\left\{k_{\script i}\right} \/|\/ k\/I\right) \/=\/ \frac {\prod\/_{\script i}{n_{\script i} \choose k_{\script i}}} {{n \choose k}}$
e indoviniamo il seme della carta successiva con probabilità
$p\left(S \/|\/ \left\{k_{\script i}\right} \/ k\/I\right) \/=\/ \frac {\max\left(n_{\script i}- k_{\script i}\right)} {n-k }$
Nel caso di un mazzo di due semi con venti carte ciascuno ottengo
$\frac {1618881562939} {68923264410} \/=\/ 23,48817\ldots$
Nel caso di un mazzo di carte da poker, quattro semi di tredici carte e uno di due (le matte)
$\frac {488039189062649921} {26465366685739716} \/=\/ 18,44067\ldots$
Nel caso di un mazzo da canasta, due semi da $78$ carte (le rosse e le nere) e uno da $6$ (le matte)
$\frac {95196356817193325395718112065240004496785758977286909} {1114973290690367403293879546259439615133129445649200} \/=\/ 85,3799\ldots$